我就废话不多说了，大家还是直接看代码吧~

import numpy as np 
kernel = np.array([1, 1, 1, 2]).reshape((2, 2))
print(kernel)
print(np.linalg.inv(kernel))

注意，Singular matrix奇异矩阵不可求逆

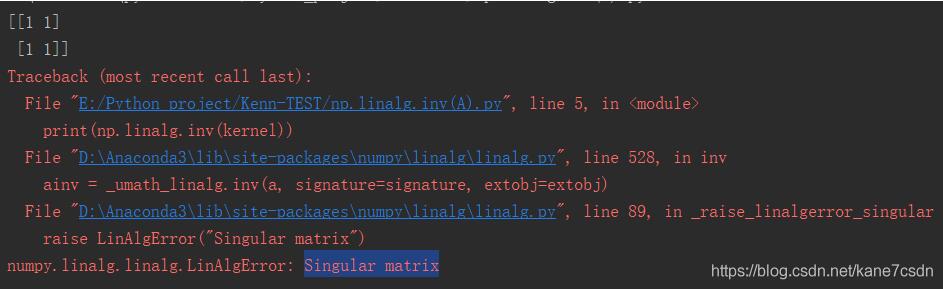
补充：python+numpy中矩阵的逆和伪逆的区别

定义：

对于矩阵A，如果存在一个矩阵B，使得AB=BA=E，其中E为与A,B同维数的单位阵，就称A为可逆矩阵（或者称A可逆），并称B是A的逆矩阵，简称逆阵。（此时的逆称为凯利逆）

矩阵A可逆的充分必要条件是|A|≠0。

伪逆矩阵是逆矩阵的广义形式。由于奇异矩阵或非方阵的矩阵不存在逆矩阵，但可以用函数pinv(A)求其伪逆矩阵。

基本语法为X=pinv(A),X=pinv(A,tol),其中tol为误差,pinv为pseudo-inverse的缩写：max(size(A))*norm(A)*eps。

函数返回一个与A的转置矩阵A' 同型的矩阵X，并且满足：AXA=A,XAX=X.此时，称矩阵X为矩阵A的伪逆，也称为广义逆矩阵。

pinv(A)具有inv(A)的部分特性，但不与inv(A)完全等同。

如果A为非奇异方阵，pinv(A)=inv(A)，但却会耗费大量的计算时间，相比较而言，inv(A)花费更少的时间。

代码如下：

1.矩阵求逆

import numpy as np
a = np.array([[1, 2], [3, 4]]) # 初始化一个非奇异矩阵(数组)
print(np.linalg.inv(a)) # 对应于MATLAB中 inv() 函数
# 矩阵对象可以通过 .I 求逆,但必须先使用matirx转化
A = np.matrix(a)
print(A.I)

2.矩阵求伪逆

import numpy as np
# 定义一个奇异阵 A
A = np.zeros((4, 4))
A[0, -1] = 1
A[-1, 0] = -1
A = np.matrix(A)
print(A)
# print(A.I) 将报错，矩阵 A 为奇异矩阵，不可逆
print(np.linalg.pinv(A)) # 求矩阵 A 的伪逆（广义逆矩阵），对应于MATLAB中 pinv() 函数

这就是矩阵的逆和伪逆的区别

截至2020/10/4，matrix函数还可以使用，但已经过时，应该是mat函数这种。

以上为个人经验，希望能给大家一个参考，也希望大家多多支持脚本之家。如有错误或未考虑完全的地方，望不吝赐教。