二分法
def sqrtb(n):
if n0: raise ValueError('n>=0')
left,right,x=0,n,n/2
while not -1e-15x*x-n1e-15:
if x*x>n:
right,x = x,left+(x-left)/2
else:
left,x = x,right-(right-x)/2
return x
求最接近算术平方根的整数
def sqrtB(x):
if x==0: return 0
#y,x=x,round(x)
left,right,ret = 1,x,0
while left=right:
mid = left + (right-left)//2
if midx/mid:
left = mid+1
ret = mid
elif mid==x/mid:
ret = mid
break
else:
right = mid-1
return ret
>>> sqrtB(9)
3
>>> sqrtB(8)
2
>>> sqrtB(9.2)
3.0
>>> sqrtB(7.8)
2.0
>>> sqrtB(4)
2
>>>
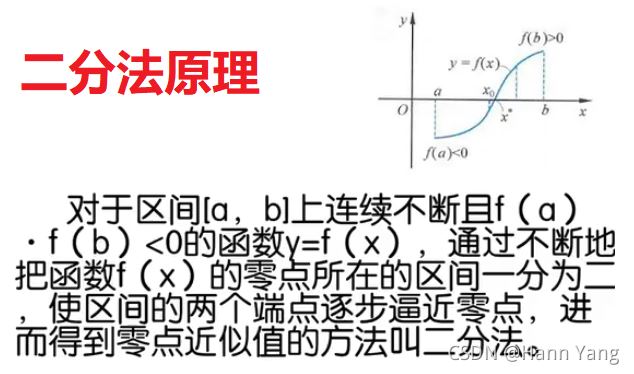
二分法原理
牛顿迭代法
def sqrtn(n):
if n0: raise ValueError('n>=0')
x = n/2
while not -1e-15x*x-n1e-15:
x = (x+n/x)/2
return x
一点小改进:不用1e-15来比较
def sqrt2(n):
x = n
while x*x>n:
x = (x+n/x)/2
return x
缺点:碰到n=7,13,...等,会进入死循环
增加判断跳出循环:
def sqrt(n):
x = n
while x*x>n:
y,x = x,(x+n/x)/2
if y==x: break
return x
# sqrt(n) n=1~25的精度测试:
0.0
-2.220446049250313e-16
0.0
0.0
0.0
0.0
0.0
-4.440892098500626e-16
0.0
-4.440892098500626e-16
0.0
0.0
4.440892098500626e-16
0.0
0.0
0.0
0.0
8.881784197001252e-16
-8.881784197001252e-16
0.0
0.0
0.0
0.0
0.0
0.0
>>>
牛顿迭代法原理
从函数意义上理解:要求函数f(x)=x²,使f(x)=num的近似解,即x²-num=0的近似解。
从几何意义上理解:要求抛物线g(x)=x²-num与x轴交点(g(x)=0)最接近的点。
假设g(x0)=0,即x0是正解,让近似解x不断逼近x0,x0 ~ x - f(x)/f'(x)
def cubeN(n):
x,y = n/3,0
while not -1e-15x-y1e-15:
y,x = x,(2/3)*x+n/(3*x*x)
return x
'''
>>> cubeN(27)
3.0
>>> cubeN(9)
2.080083823051904
>>>
'''
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注脚本之家的更多内容!
您可能感兴趣的文章:- Python编程实现二分法和牛顿迭代法求平方根代码
- Python用二分法求平方根的案例
- Python基于二分查找实现求整数平方根的方法
- Python求算数平方根和约数的方法汇总
- Python中利用sqrt()方法进行平方根计算的教程
 咨 询 客 服
咨 询 客 服