今天来分享一下图,这是一种比较复杂的非线性数据结构,之所以复杂是因为他们的数据元素之间的关系是任意的,而不像树那样 被几个性质定理框住了,元素之间的关系还是比较明显的,图的使用范围很广的,比如网络爬虫,求最短路径等等,不过大家也不要胆怯,
越是复杂的东西越能体现我们码农的核心竞争力。
既然要学习图,得要遵守一下图的游戏规则。
一: 概念
图是由“顶点”的集合和“边”的集合组成。记作:G=(V,E);
1> 无向图
就是“图”中的边没有方向,那么(V1,V2)这条边自然跟(V2,V1)是等价的,无向图的表示一般用”圆括号“。
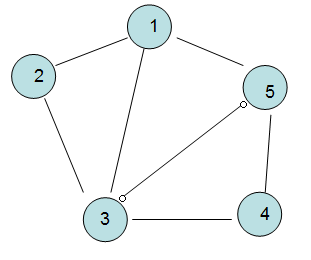
2> 有向图
“图“中的边有方向,自然V1,V2>这条边跟V2,V1>不是等价的,有向图的表示一般用"尖括号"表示。
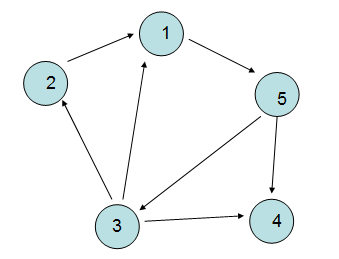
3> 邻接点
一条边上的两个顶点叫做邻接点,比如(V1,V2),(V1,V3),(V1,V5),只是在有向图中有一个“入边,出边“的
概念,比如V3的入边为V5,V3的出边为V2,V1,V4。
4> 顶点的度
这个跟“树”中的度的意思一样。不过有向图中也分为“入度”和“出度”两种,这个相信大家懂的。
5> 完全图
每两个顶点都存在一条边,这是一种完美的表现,自然可以求出边的数量。
无向图:edges=n(n-1)/2;
有向图:edges=n(n-1); //因为有向图是有边的,所以必须在原来的基础上"X2"。
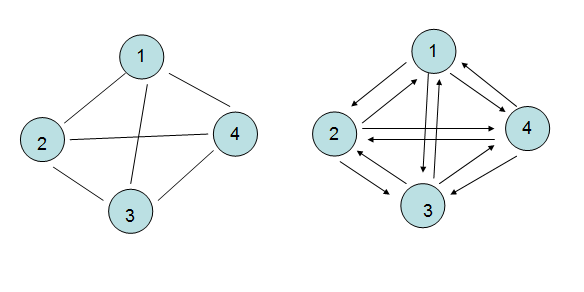
6> 子图
如果G1的所有顶点和边都在G2中,则G1是G2的子图,具体不说了。
7> 路径,路径长度和回路(这些概念还是比较重要的)
路径: 如果Vm到Vn之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度: 一条路径中“边的数量”。
简单路径: 若一条路径上顶点不重复出现,则是简单路径。
回路: 若路径的第一个顶点和最后一个顶点相同,则是回路。
简单回路: 第一个顶点和最后一个顶点相同,其它各顶点都不重复的回路则是简单回路。
8> 连通图和连通分量(针对无向图而言的)
连通图: 无向图中,任意两个顶点都是连通的则是连通图,比如V1,V2,V4之间。
连通分量: 无向图的极大连通子图就是连通分量,一般”连通分量“就是”图“本身,除非是“非连通图”,
如下图就是两个连通分量。
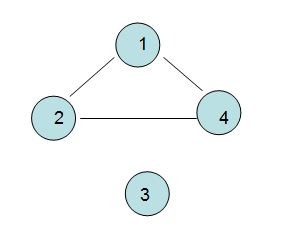
9> 强连通图和强连通分量(针对有向图而言)
这里主要注意的是“方向性“,V4可以到V3,但是V3无法到V4,所以不能称为强连通图。
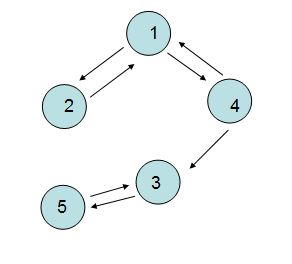
10> 网
边上带有”权值“的图被称为网。很有意思啊,呵呵。
二:存储
图的存储常用的是”邻接矩阵”和“邻接表”。
邻接矩阵: 手法是采用两个数组,一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息,
缺点就是比较耗费空间。
邻接表: 改进后的“邻接矩阵”,缺点是不方便判断两个顶点之间是否有边,但是相比节省空间。
三: 创建图
这里我们就用邻接矩阵来保存图,一般的操作也就是:①创建,②遍历
复制代码 代码如下:
#region 邻接矩阵的结构图
/// summary>
/// 邻接矩阵的结构图
/// /summary>
public class MatrixGraph
{
//保存顶点信息
public string[] vertex;
//保存边信息
public int[,] edges;
//深搜和广搜的遍历标志
public bool[] isTrav;
//顶点数量
public int vertexNum;
//边数量
public int edgeNum;
//图类型
public int graphType;
/// summary>
/// 存储容量的初始化
/// /summary>
/// param name="vertexNum">/param>
/// param name="edgeNum">/param>
/// param name="graphType">/param>
public MatrixGraph(int vertexNum, int edgeNum, int graphType)
{
this.vertexNum = vertexNum;
this.edgeNum = edgeNum;
this.graphType = graphType;
vertex = new string[vertexNum];
edges = new int[vertexNum, vertexNum];
isTrav = new bool[vertexNum];
}
}
#endregion
1> 创建图很简单,让用户输入一些“边,点,权值"来构建一下图
复制代码 代码如下:
#region 图的创建
/// summary>
/// 图的创建
/// /summary>
/// param name="g">/param>
public MatrixGraph CreateMatrixGraph()
{
Console.WriteLine("请输入创建图的顶点个数,边个数,是否为无向图(0,1来表示),已逗号隔开。");
var initData = Console.ReadLine().Split(',').Select(i => int.Parse(i)).ToList();
MatrixGraph graph = new MatrixGraph(initData[0], initData[1], initData[2]);
Console.WriteLine("请输入各顶点信息:");
for (int i = 0; i graph.vertexNum; i++)
{
Console.Write("\n第" + (i + 1) + "个顶点为:");
var single = Console.ReadLine();
//顶点信息加入集合中
graph.vertex[i] = single;
}
Console.WriteLine("\n请输入构成两个顶点的边和权值,以逗号隔开。\n");
for (int i = 0; i graph.edgeNum; i++)
{
Console.Write("第" + (i + 1) + "条边:\t");
initData = Console.ReadLine().Split(',').Select(j => int.Parse(j)).ToList();
int start = initData[0];
int end = initData[1];
int weight = initData[2];
//给矩阵指定坐标位置赋值
graph.edges[start - 1, end - 1] = weight;
//如果是无向图,则数据呈“二,四”象限对称
if (graph.graphType == 1)
{
graph.edges[end - 1, start - 1] = weight;
}
}
return graph;
}
#endregion
2>广度优先
针对下面的“图型结构”,我们如何广度优先呢?其实我们只要深刻理解"广搜“给我们定义的条条框框就行了。 为了避免同一个顶点在遍历时被多
次访问,可以将”顶点的下标”存放在sTrav[]的bool数组,用来标识是否已经访问过该节点。
第一步:首先我们从isTrav数组中选出一个未被访问的节点,如V1。
第二步:访问V1的邻接点V2,V3,V5,并将这三个节点标记为true。
第三步:第二步结束后,我们开始访问V2的邻接点V1,V3,但是他们都是被访问过的。
第四步:我们从第二步结束的V3出发访问他的邻接点V2,V1,V5,V4,还好V4是未被访问的,此时标记一下。
第五步:我们访问V5的邻接点V1,V3,V4,不过都是已经访问过的。
第六步:有的图中通过一个顶点的“广度优先”不能遍历所有的顶点,此时我们重复(1-5)的步骤就可以最终完成广度优先遍历。

复制代码 代码如下:
#region 广度优先
/// summary>
/// 广度优先
/// /summary>
/// param name="graph">/param>
public void BFSTraverse(MatrixGraph graph)
{
//访问标记默认初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍历每个顶点
for (int i = 0; i graph.vertexNum; i++)
{
//广度遍历未访问过的顶点
if (!graph.isTrav[i])
{
BFSM(ref graph, i);
}
}
}
/// summary>
/// 广度遍历具体算法
/// /summary>
/// param name="graph">/param>
public void BFSM(ref MatrixGraph graph, int vertex)
{
//这里就用系统的队列
Queueint> queue = new Queueint>();
//先把顶点入队
queue.Enqueue(vertex);
//标记此顶点已经被访问
graph.isTrav[vertex] = true;
//输出顶点
Console.Write(" ->" + graph.vertex[vertex]);
//广度遍历顶点的邻接点
while (queue.Count != 0)
{
var temp = queue.Dequeue();
//遍历矩阵的横坐标
for (int i = 0; i graph.vertexNum; i++)
{
if (!graph.isTrav[i] graph.edges[temp, i] != 0)
{
graph.isTrav[i] = true;
queue.Enqueue(i);
//输出未被访问的顶点
Console.Write(" ->" + graph.vertex[i]);
}
}
}
}
#endregion
3> 深度优先
同样是这个图,大家看看如何实现深度优先,深度优先就像铁骨铮铮的好汉,遵循“能进则进,不进则退”的原则。
第一步:同样也是从isTrav数组中选出一个未被访问的节点,如V1。
第二步:然后一直访问V1的邻接点,一直到走头无路的时候“回溯”,路线为V1,V2,V3,V4,V5,到V5的时候访问邻接点V1,发现V1是访问过的,
此时一直回溯的访问直到V1。
第三步: 同样有的图中通过一个顶点的“深度优先”不能遍历所有的顶点,此时我们重复(1-2)的步骤就可以最终完成深度优先遍历。

复制代码 代码如下:
#region 深度优先
/// summary>
/// 深度优先
/// /summary>
/// param name="graph">/param>
public void DFSTraverse(MatrixGraph graph)
{
//访问标记默认初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍历每个顶点
for (int i = 0; i graph.vertexNum; i++)
{
//广度遍历未访问过的顶点
if (!graph.isTrav[i])
{
DFSM(ref graph, i);
}
}
}
#region 深度递归的具体算法
/// summary>
/// 深度递归的具体算法
/// /summary>
/// param name="graph">/param>
/// param name="vertex">/param>
public void DFSM(ref MatrixGraph graph, int vertex)
{
Console.Write("->" + graph.vertex[vertex]);
//标记为已访问
graph.isTrav[vertex] = true;
//要遍历的六个点
for (int i = 0; i graph.vertexNum; i++)
{
if (graph.isTrav[i] == false graph.edges[vertex, i] != 0)
{
//深度递归
DFSM(ref graph, i);
}
}
}
#endregion
#endregion
最后上一下总的代码
复制代码 代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace MatrixGraph
{
public class Program
{
static void Main(string[] args)
{
MatrixGraphManager manager = new MatrixGraphManager();
//创建图
MatrixGraph graph = manager.CreateMatrixGraph();
manager.OutMatrix(graph);
Console.Write("广度递归:\t");
manager.BFSTraverse(graph);
Console.Write("\n深度递归:\t");
manager.DFSTraverse(graph);
Console.ReadLine();
}
}
#region 邻接矩阵的结构图
/// summary>
/// 邻接矩阵的结构图
/// /summary>
public class MatrixGraph
{
//保存顶点信息
public string[] vertex;
//保存边信息
public int[,] edges;
//深搜和广搜的遍历标志
public bool[] isTrav;
//顶点数量
public int vertexNum;
//边数量
public int edgeNum;
//图类型
public int graphType;
/// summary>
/// 存储容量的初始化
/// /summary>
/// param name="vertexNum">/param>
/// param name="edgeNum">/param>
/// param name="graphType">/param>
public MatrixGraph(int vertexNum, int edgeNum, int graphType)
{
this.vertexNum = vertexNum;
this.edgeNum = edgeNum;
this.graphType = graphType;
vertex = new string[vertexNum];
edges = new int[vertexNum, vertexNum];
isTrav = new bool[vertexNum];
}
}
#endregion
/// summary>
/// 图的操作类
/// /summary>
public class MatrixGraphManager
{
#region 图的创建
/// summary>
/// 图的创建
/// /summary>
/// param name="g">/param>
public MatrixGraph CreateMatrixGraph()
{
Console.WriteLine("请输入创建图的顶点个数,边个数,是否为无向图(0,1来表示),已逗号隔开。");
var initData = Console.ReadLine().Split(',').Select(i => int.Parse(i)).ToList();
MatrixGraph graph = new MatrixGraph(initData[0], initData[1], initData[2]);
Console.WriteLine("请输入各顶点信息:");
for (int i = 0; i graph.vertexNum; i++)
{
Console.Write("\n第" + (i + 1) + "个顶点为:");
var single = Console.ReadLine();
//顶点信息加入集合中
graph.vertex[i] = single;
}
Console.WriteLine("\n请输入构成两个顶点的边和权值,以逗号隔开。\n");
for (int i = 0; i graph.edgeNum; i++)
{
Console.Write("第" + (i + 1) + "条边:\t");
initData = Console.ReadLine().Split(',').Select(j => int.Parse(j)).ToList();
int start = initData[0];
int end = initData[1];
int weight = initData[2];
//给矩阵指定坐标位置赋值
graph.edges[start - 1, end - 1] = weight;
//如果是无向图,则数据呈“二,四”象限对称
if (graph.graphType == 1)
{
graph.edges[end - 1, start - 1] = weight;
}
}
return graph;
}
#endregion
#region 输出矩阵数据
/// summary>
/// 输出矩阵数据
/// /summary>
/// param name="graph">/param>
public void OutMatrix(MatrixGraph graph)
{
for (int i = 0; i graph.vertexNum; i++)
{
for (int j = 0; j graph.vertexNum; j++)
{
Console.Write(graph.edges[i, j] + "\t");
}
//换行
Console.WriteLine();
}
}
#endregion
#region 广度优先
/// summary>
/// 广度优先
/// /summary>
/// param name="graph">/param>
public void BFSTraverse(MatrixGraph graph)
{
//访问标记默认初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍历每个顶点
for (int i = 0; i graph.vertexNum; i++)
{
//广度遍历未访问过的顶点
if (!graph.isTrav[i])
{
BFSM(ref graph, i);
}
}
}
/// summary>
/// 广度遍历具体算法
/// /summary>
/// param name="graph">/param>
public void BFSM(ref MatrixGraph graph, int vertex)
{
//这里就用系统的队列
Queueint> queue = new Queueint>();
//先把顶点入队
queue.Enqueue(vertex);
//标记此顶点已经被访问
graph.isTrav[vertex] = true;
//输出顶点
Console.Write(" ->" + graph.vertex[vertex]);
//广度遍历顶点的邻接点
while (queue.Count != 0)
{
var temp = queue.Dequeue();
//遍历矩阵的横坐标
for (int i = 0; i graph.vertexNum; i++)
{
if (!graph.isTrav[i] graph.edges[temp, i] != 0)
{
graph.isTrav[i] = true;
queue.Enqueue(i);
//输出未被访问的顶点
Console.Write(" ->" + graph.vertex[i]);
}
}
}
}
#endregion
#region 深度优先
/// summary>
/// 深度优先
/// /summary>
/// param name="graph">/param>
public void DFSTraverse(MatrixGraph graph)
{
//访问标记默认初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍历每个顶点
for (int i = 0; i graph.vertexNum; i++)
{
//广度遍历未访问过的顶点
if (!graph.isTrav[i])
{
DFSM(ref graph, i);
}
}
}
#region 深度递归的具体算法
/// summary>
/// 深度递归的具体算法
/// /summary>
/// param name="graph">/param>
/// param name="vertex">/param>
public void DFSM(ref MatrixGraph graph, int vertex)
{
Console.Write("->" + graph.vertex[vertex]);
//标记为已访问
graph.isTrav[vertex] = true;
//要遍历的六个点
for (int i = 0; i graph.vertexNum; i++)
{
if (graph.isTrav[i] == false graph.edges[vertex, i] != 0)
{
//深度递归
DFSM(ref graph, i);
}
}
}
#endregion
#endregion
}
}
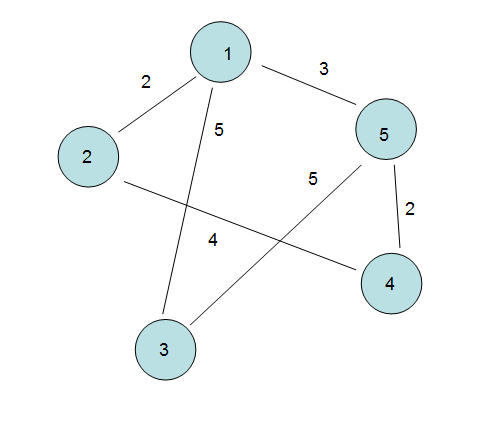
代码中我们构建了如下的“图”。
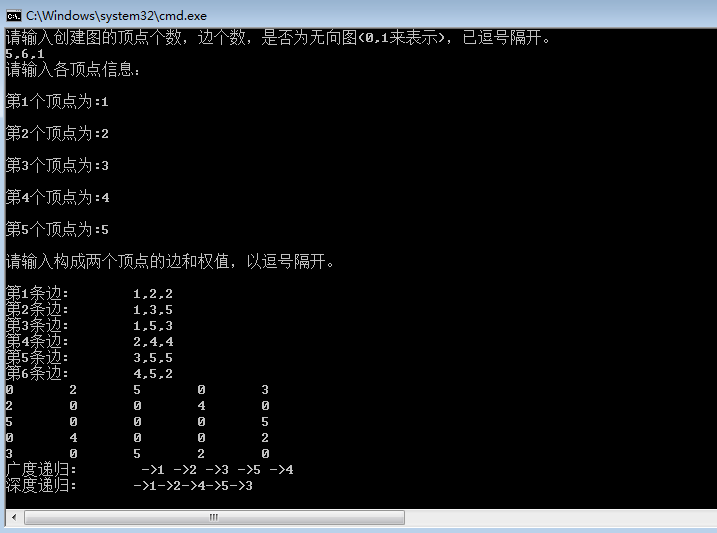
您可能感兴趣的文章:- 算法系列15天速成——第十三天 树操作【下】
- 算法系列15天速成 第十二天 树操作【中】
- 算法系列15天速成 第十一天 树操作(上)
- 算法系列15天速成 第十天 栈
- 算法系列15天速成 第八天 线性表【下】
- 算法系列15天速成 第九天 队列
- 算法系列15天速成 第七天 线性表【上】
- 算法系列15天速成 第六天 五大经典查找【下】
- 算法系列15天速成 第五天 五大经典查找【中】
- 算法系列15天速成 第四天 五大经典查找【上】
- 算法系列15天速成 第三天 七大经典排序【下】
- 算法系列15天速成 第二天 七大经典排序【中】
- 算法系列15天速成 第一天 七大经典排序【上】
- 算法系列15天速成——第十五天 图【下】(大结局)
 咨 询 客 服
咨 询 客 服