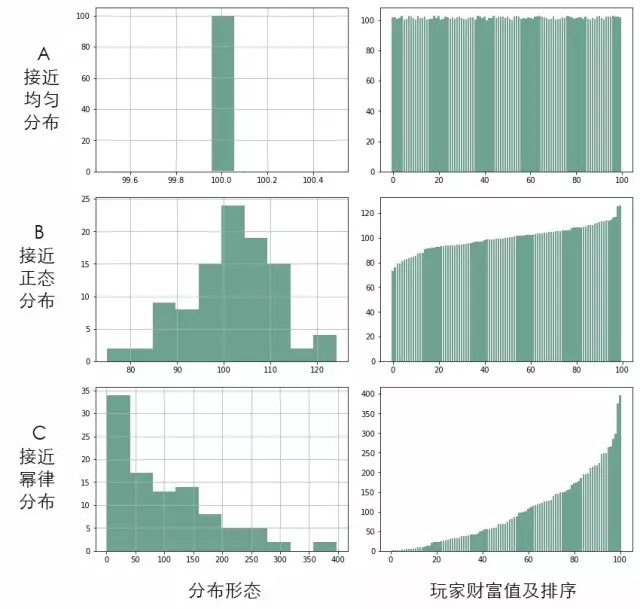
比来在知乎上看到一个很有趣的问题：房间里有 100 个人，每人都有 100 元钱，他们在玩一个游戏。每轮游戏中，每个人都要拿出一元钱随机给另一个人，最后这 100 个人的财富分布是怎样的？

以下是三个差别的答案，你认为最终结果会是怎样的呢？

我们不妨事把这场游戏视作社会财富分配的简化模型，从而模拟这个世界的运行规律。我们假设：每个人在 18 岁带着 100 元的初始资金开始玩游戏，，每天玩一次，一直玩到 65 岁退休。“每天拿出一元钱”可理解为基本的日常消费，“获得财富的概率随机”是为了……嗯……简化模型。以此计算，人一生要玩 17000 次游戏，即获得 17000 次财富分配的机会。

下面我们来回答一下。

在上述规则下，游戏运行 17000 次的结果如下图所示：

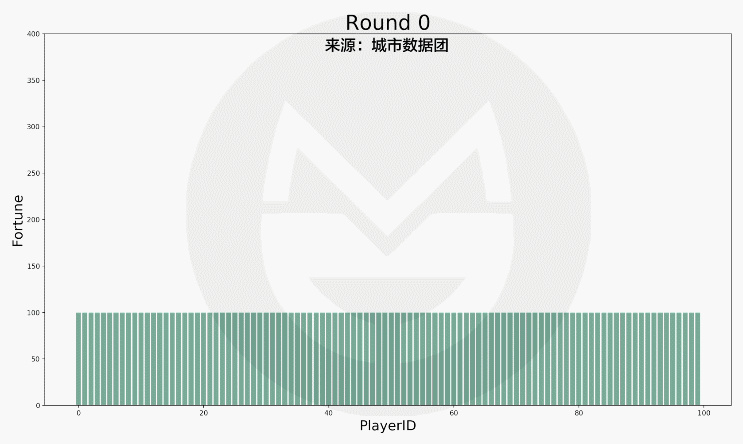
（说明：1.上图中横轴标签代表一个玩家的编号，柱子的凹凸变动反映该玩家财富值的变革。2. 当某人的财富值降到 0 元时，他在该轮无需拿出 1 元钱给别人，但仍然有机会得到别人给出的钱。）

可以看到，每个玩家财富值的变动是极为剧烈的。为了便利描述整个社会财富的分配状况，我们又根据财富值的排序做了下图：

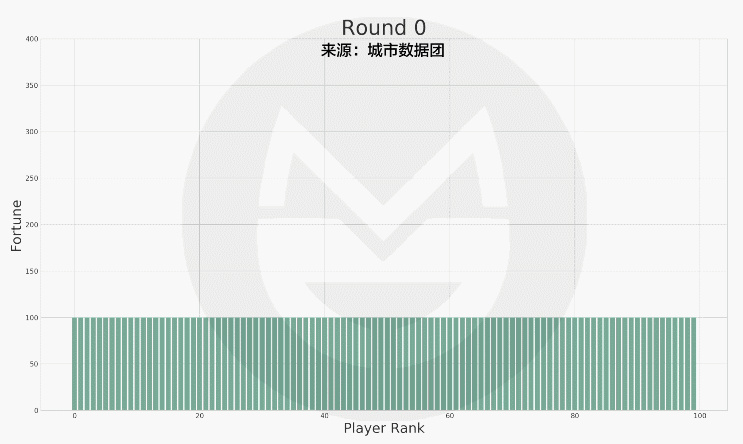
（说明：上图中横轴标签代表玩家排序（非编号），排序越高的财富越多。初始时所有人的财富值相等，随着游戏的进行，财富值差距越来越大。）

没错，财富的分配接近于幂律分布（结论只是程序模拟，而非数学精确求解）。最后，社会将有很少的富人和很多的穷人：

最富有的人的财富值约为初始财富的3. 5 倍；

top10%的富人掌握着大约30%的财富，top20%的富人掌握着大约50%的财富；60%的人的财富将缩水到 100 元以下。

就这样，大部分人的钱跑进了少部分人的口袋里。即使在最公平的规则下，世界依然展现出了残酷的一面。

在此基础上，我们又设计了更多的情景，同样用程序进行了模拟。

允许借债会让世界变得好一点吗？

在现实社会中，情境会更复杂一些。好比说，当我们没钱了，还可以找亲友、找银行、找投资人借债，说不定哪天就东山再起了呢。在允许借债的情况下，游戏结果如下图所示（排序后结果）：

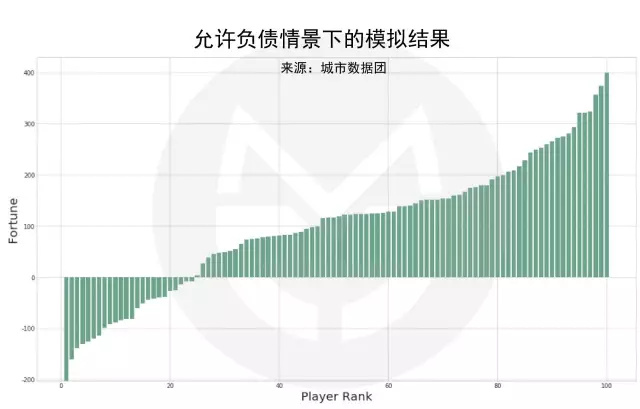
结果表白：

游戏结束时，最富有的人的财富值约为初始财富的 4 倍；

top10%的富人掌握着大约33%的财富，top20%的富人掌握着大约56%的财富；大约25%的人背负着债务，最高负债约为 200 元。

没错。借债虽然能让我们在走投无路时多一些周转余地，但最终会让穷人变得更穷。

屌丝真能逆袭吗？

我们以所有玩家财富值的尺度差来衡量社会贫富分化程度，定时间序列做出图来长这样：

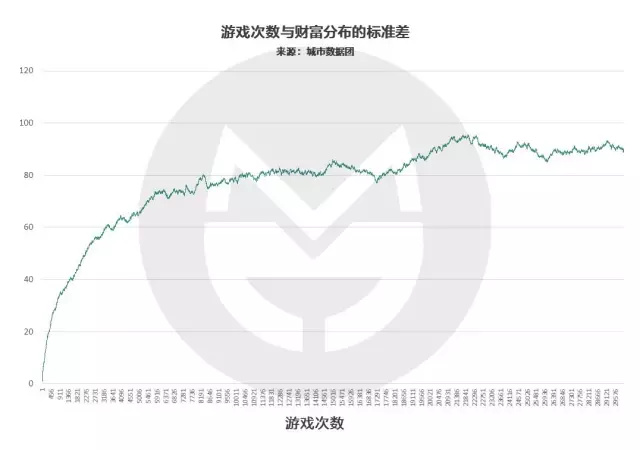
（说明：横轴体现游戏轮数，纵轴体现社会财富的尺度差）

可以看到，游戏早期的尺度差变动最为激烈，而在6000- 6500 轮游戏后，尺度差的变革趋于平缓，也就是社会财富分布的总体形态趋于不变了。根据我们设定的游戏与人生的对应规则，这时玩家年龄为 35 岁。

这个结果告诉我们， 35 岁之前，人与人之间的差距已经完全拉开了。

进一步看，如果一个人在 35 岁时破产，还有没有可能逆袭呢？

本次模拟结果中，有 15 个人在 35 岁的最后一天时处于破产（负债）状态，而他们在此后的财富值及排名如下图所示：

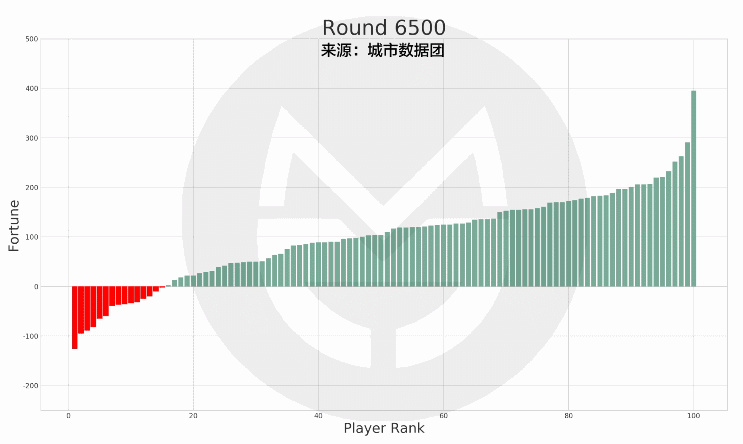
（说明：上图中的红色柱子为在 35 岁时破产的玩家，绿色柱子为其他玩家。红色柱子在纵轴上的高度变革体现其财富值变革，在横轴上的位置变革体现其排名变革。）

可以看到，当这 15 个人在 65 岁退休时，有 7 人仍然处于破产状态；有 8 人还清债务并有了财富积累，但离富豪仍有相当差距。

看来，以 35 岁为界，虽然破产以后，仍有一半概率回复到普通人的生活，但想要逆袭暴富，却是相当困难的。

所以，发财要趁早，大龄屌丝逆袭更像是一个传说。