起因
今天在学习《HTML5+Javascript动画基础》这本书的时候,在第八章的第三节讲到如何用三个弹簧连接三个点来做拉伸运动。
在做完例子之后,就想到如果是四个点,五个点,怎么样。
就改写了一下代码,把点的数目变量化。最终的效果是能实现各个点最终的拉伸运动到平衡,可是点之间的连线不是很好看,有些是交叉的。
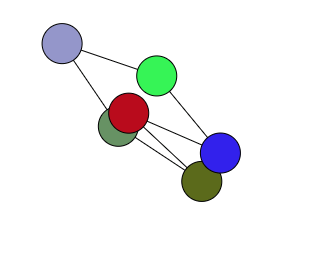
于是就想着能不能优化这一块。
旋转连线
前面例子里面的点,都是随机位置,所以连线不可控。所以想先从这块着手。
先以某一个点为参照点,获得其他点相对于这个点的角度。
然后按照角度从小到大的去连接这些点,这样就能画出一个正常的多边形了。
大致实现代码如下:
let balls = [];
let ballNum = 6;
let firstBall = null;
while(ballNum--) {
let ball = new Ball(20, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
balls.push(ball)
if (!firstBall) {
firstBall = ball
ball.angle = 0
} else {
const dx = ball.x - firstBall.x,
dy = ball.y - firstBall.y;
ball.angle = Math.atan2(dy, dx);
}
}
// 尝试让球连线是一个正多边形
balls = balls.sort((ballA, ballB) => {
return ballA.angle - ballB.angle
})
这样在最后绘制连线的时候,遍历数组就能按照角度从小到大来绘制了。
效果如下:
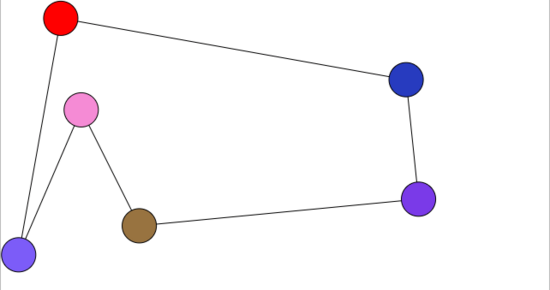
这样是能极大的减少交叉线的情况,可还是无法完全避免。
接下来,想尝试优化这个方案,比如angle用Math.abs来取正,或者每一个点都找夹角最小的点来连线。可是结果都不行,无法避免交叉线。
基于中心点旋转
后面又想到一个思路,如果能确定多边形的中心点,那么分别计算所有点相对于中心点的夹角,就能以顺时针或者逆时针来连接这些点。
可是在网上找了半天,所有点算法里面,都是要求有一系列按某个时针顺序排列的点。
可是如果我有这些点,就已经能绘制多边形了。只好放弃
X轴两极点分割
无奈之下只好找Google,然后就发现了知乎上的一个答案挺好的: 如何将平面上无序的一组点连成一个简单多边形?
具体算法描述,大家看那个答案就好,我就不赘述了。
不过在连接上链和下链的时候,其实只要保证上链是X轴降序连接,下链是X轴升序连接即可(以逆时针方向绘制)。至于X轴相同的点,不管是优先Y轴大的还是小的都可以。
实现的时候,是严格按照答案里面的算法实现的。
在判断一个点是属于上链还是下链的时候,一开始想的是基于两点确定直线的函数方程,再引入点的坐标来计算。不过后面想到,所有的点都以最左边的极点来计算斜角,然后根据角度大小来划分,视觉上更好理解。
大致代码如下:
let balls = [];
let tempBalls = [];
let ballNum = 6;
let isDragingBall = false;
while(ballNum--) {
let ball = new Ball(10, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
tempBalls.push(ball)
}
// 让点按X轴升序排序
tempBalls = tempBalls.sort((ballA, ballB) => {
return ballA.x - ballB.x
})
// 找X轴左右极点
let firstBall = tempBalls[0],
lastBall = tempBalls[tempBalls.length -1];
let smallXBalls = tempBalls.filter(ball => ball.x === firstBall.x),
bigXBalls = tempBalls.filter(ball => ball.x === lastBall.x)
// 处理左右极点有多个的情况
if (smallXBalls.length > 1) {
smallXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
if (bigXBalls.length > 1) {
bigXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
firstBall = smallXBalls[0]
lastBall = bigXBalls[0]
// 获得极点连线的角度
let splitLineAngle = Math.atan2(lastBall.y - firstBall.y, lastBall.x - firstBall.x);
let upperBalls = [],
lowerBalls = [];
// 所有其他点跟firstBall计算角度
// 大于splitLineAngle的都是下链
// 其他是上链
tempBalls.forEach(ball => {
if (ball === firstBall || ball === lastBall) {
return false
}
let angle = Math.atan2(ball.y - firstBall.y, ball.x - firstBall.x);
if (angle > splitLineAngle) {
lowerBalls.push(ball)
} else {
upperBalls.push(ball)
}
})
// 处理X轴相同情况的排序
lowerBalls = lowerBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballA.x - ballB.x
}
return ballB.y - ballA.y
})
upperBalls = upperBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballB.x - ballA.x
}
return ballB.y - ballB.x
})
// 逆时针连接所有的点
balls = [firstBall].concat(lowerBalls, [lastBall], upperBalls)
balls = balls.map((ball, i) => {
ball.text = i + 1;
return ball
})
最终返回的balls,就是按逆时针排序的多边形的点了。
效果如下:
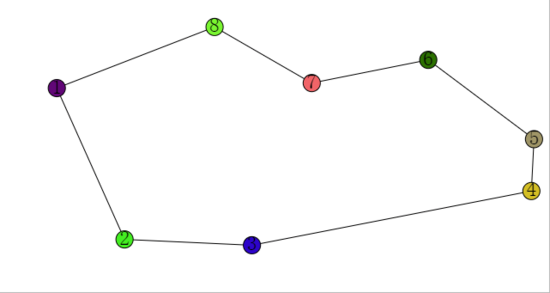
各个球的内部状态如下:

以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。
 咨 询 客 服
咨 询 客 服