客户支付能力是指客户能够以货币形式支付货物款项的能力,是构成市场的三要素之一,又是客户资格审查的主要内容,同时还是防止推销人员上当受骗的主要方法。
(1)客户支付能力审核的目的
1)寻找合格的客户。一些客户的潜在需求不等于现实的市场购买需求,更不等于客户的现实购买行为。只有那些具有支付能力的需求,才能构成现实的市场需求和现实的客户购买行为。有支付能力的客户才是合格的客户。不合格的客户不能纳入推销计划之中。
2)提高推销效率。在构成市场的三要素中,客户支付能力是一个关键的、稳定的、相对缺乏弹性的因素,也是推销人员最担心的一个因素。只有通过事先的审查,把那些对产品拥有需求,又拥有足够支付能力的客户作为推销的具体对象,才能提高推销效率。
3)能更好地满足客户需求。支付能力是目前影响客户消费与购买的主要因素。拥有不同支付能力的客户,往往存在着不同的需求。了解客户的支付能力并加以分析,才可以实现量体裁衣量身定做,分别满足不同客户的不同层次的需求。
4)防止与避免货款损失。随着市场经济的发展与竞争的加剧,商业欺诈行为时有发生。对推销对象的购买资格、信用审查不够,是造成巨大损失的主要原因。因此,推销人员不仅要了解对方现时是否有足够的支付能力,而且要了解对方在回收货款方面的态度。
(2)个人客户的购买能力审查
个人客户的购买能力审查主要是从影响消费者购买力的各种因素,如实际收入、家庭总支出、消费储蓄与信贷等几个方面进行审查。其中,实际收入的多少决定了个人客户市场购买水平的高低,也是影响高档耐用消费品、旅游商品销售的主要因素。这部分收入越多,人们的购买力就越强,人们的消费水平也越高,企业的营销机会也就越多。另外,客户的购买力除了受实际收入的影响外,还要受家庭总支出、家庭储蓄和信贷情况等因素的直接影响。例如,当前各种形式的赊销、分期付款、延期付款购物越来越多,因为它允许人们购买超过自己实际购买力的商品。所以有些年轻人,虽然收入不高,但是由于提前贷款消费的意识比较强,也可能具有一定的购买能力,从而有可能被推销人员确定为目标对象。
当然,在消费信贷发展比较好的行业,例如房地产行业、汽车行业、其他大件耐用品行业的购销活动中,也需要对个人消费者的支付能力进行审查。
(3)团体客户的购买力审查
购买力审查的重点对象是组织与企业购买者,他们是客户支付能力审查的主要对象。
推销人员对团体客户购买力的审查涉及团体客户的生产状况、经营状况、资金状况、财务状况、信用状况等方面。这里主要介绍团体客户短期偿债能力和营运能力的分析。
1)短期偿债能力分析。
短期偿债能力又称支付能力,是企业以其流动资产偿还流动负债的能力。它反映企业偿付日常到期债务的实力。企业能否及时偿还到期的流动负债,是反映企业财务状况好坏的重要标志。企业如果短期偿债能力较弱,供应商将很难甚至无法收回货款。反映企业短期偿债能力的财务指标主要有以下几种。
•流动比率
流动比率是流动资产与流动负债之比,用来衡量企业的短期能力,计算公式为:
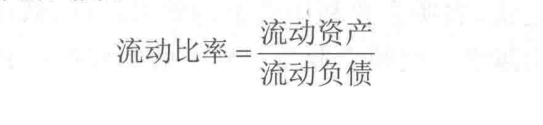
一般来讲,流动比率的结果在2左右比较合适。流动比率越高,说明企业偿还流动负债的能力越强,流动负债得到偿还的保障越大。但过高的流动比率也并非好现象,应检查资产结构是否不合理,或者是募集的长期资金没有尽快投入使用,或者是其他原因。
•速动比率
速动比率是速动资产和流动负债之比,其中的速动资产是指流动资产中能够迅速转变为现金的资产,主要包括货币资金、短期投资、应收账款和应收票据。其计算公式为:

一般来讲,速动比率的结果在1左右比较合适。速动比率越高,说明企业偿还流动负债的能力越强;低于1的速动比率被认为是短期偿债能力偏低。但速动比率过高也不好,在这种情况下企业会因现金及应收账款占用过多,而增加企业的机会成本。
•现金比率
除了以上两个指标之外,还有一个指标一一现金比率,是企业现金类资产与流动负债的比率,即现金比率二现金类资产-流动负债。现金比率是衡量企业即时偿付债务能力的比率,在反映企业短期变现能力方面,可以弥补以上两个指标的不足,能更为稳健地衡量企业的短期偿债能力。一般来说,现金比率在20%以上为好。现金比率越高,说明现金类资产在流动资产中所占比例较大,企业应急能力较强,举债能力则较大。
上述三个指标都能反映企业短期偿债能力。但企业的经营状况总是在不断变化的,要科学、合理、准确地评价企业的短期偿债能力,必须将上述三个指标结合起来综合考察。
2)营运能力分析。
营运能力通过企业生产经营资金周转速度的有关指标反映企业资金利用的效率。企业生产经营资金周转的速度越快,表明企业利用资金的效果越好,效率越高,企业短期偿债能力越强。反映企业营运能力的主要指标如下。
•应收账款周转率
应收账款周转率是指年度内应收账款转换为现金的平均次数,其计算公式为:

一般而言,应收账款周转率越高,应收账款周转天数就越短,说明应收账款的回收就越快,可以减少坏账损失。该指标同时还考察了企业的信用管理能力,如果该比率的计算结果与行业平均值偏离过大,应考虑公司的信用政策是否合理,或是否还有其他原因。
•存货周转率
存货周转率是衡量和评价企业购入存货、投入生产、销售收回等各环节管理状况的综合性指标,也称存货的周转次数。其计算公式为:

存货周转率可以反映企业的销售效率和存货使用效率。一般来讲,存货周转率越高越好。存货周转率越高,表明存货变现的速度越快,周转额越大,资金占用水平越低。
•流动资产周转率
流动资产周转率是企业主营业务收入与平均流动资产之比,其计算公式为:

流动资产周转率反映了流动资产的利用效率。结果越大,流动资产的利用效率越好。
 咨 询 客 服
咨 询 客 服