Python机器学习之Kmeans基础算法-巨人网络通讯

Python机器学习之Kmeans基础算法

一、K-means基础算法简介

k-means算法是一种聚类算法，所谓聚类，即根据相似性原则，将具有较高相似度的数据对象划分至同一类簇，将具有较高相异度的数据对象划分至不同类簇。聚类与分类最大的区别在于，聚类过程为无监督过程，即待处理数据对象没有任何先验知识，而分类过程为有监督过程，即存在有先验知识的训练数据集。

二、算法过程

K-means中心思想：事先确定常数K，常数K意味着最终的聚类（或者叫簇）类别数，首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，接着，重新计算每个类的质心(即为类中心)，重复这样的过程，直到质心不再改变，最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

1.聚类算法：

是一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。
聚类算法与分类算法最大的区别是：聚类算法是无监督的学习算法，而分类算法属于监督的学习
算法，分类是知道结果的。
在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

2.聚类：

物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。

3.簇：

本算法中可以理解为，把数据集聚类成 k 类，即 k 个簇。

4.质心：

指各个类别的中心位置，即簇中心。

5.距离公式：

常用的有：欧几里得距离（欧氏距离）、曼哈顿距离、闵可夫斯基距离等。

三、文字步骤

1.给定一个待处理的数据集

2.选择簇的个数k（kmeans算法传递超参数的时候，只需设置最大的K值）

3.任意产生k个簇，生成K个簇的中心,记 K 个簇的中心分别为 c 1 , c 2 , . . . , c k c1,c2,...,ck c1,c2,...,ck；每个簇的样本数量为 N 1 , N 2 , . . . , N 3 N1,N2,...,N3 N1,N2,...,N3。

4.通过欧几里得距离公式计算各点到各质心的距离，把每个点划分给与其距离最近的质心，从而初步把数据集分为了 K 类点。

5.更新质心：通过下面的公式来更新每个质心。就是，新的质心的值等于当前该质心所属簇的所有点的平均值。 c j = 1 N j ∑ i = 1 N j x i , y i c_{j}=\frac{1}{N_{j}}\sum_{i=1}^{N{j}}x_{i},y_{i} cj=Nj1i=1∑Njxi,yi

6.重复以上步骤直到满足收敛要求。（通常就是确定的中心点不再改变。）

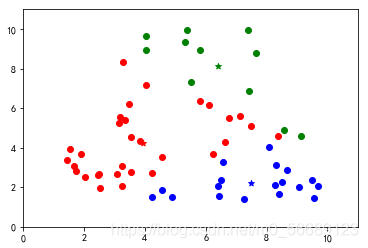
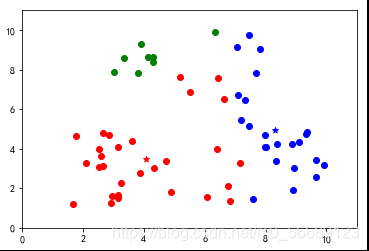
四、图形展示

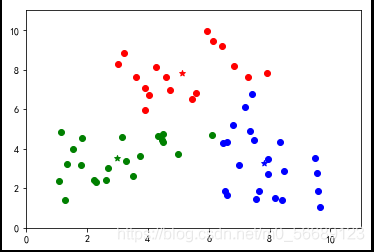
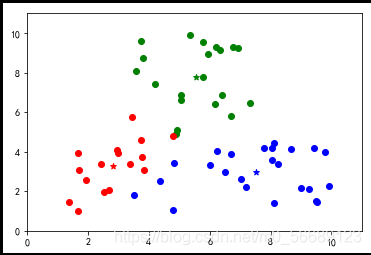
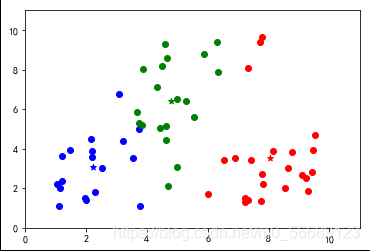
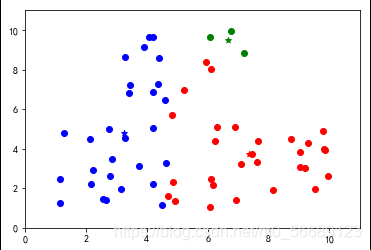
按照上述步骤我们可以更好地理解分类过程；

五、代码实现

x 轴数据],[存储 y 轴数据]]
for i in range(m):
    if i  m/3: 
        data[0].append(uniform(1,5))#随机设定
        data[1].append(uniform(1,5))
    elif i  2*m/3:
        data[0].append(uniform(6,10))
        data[1].append(uniform(1,5))
    else:
        data[0].append(uniform(3,8))
        data[1].append(uniform(5,10))
#将创建的数据集画成散点图
plt.scatter(data[0],data[1])
plt.xlim(0,11)
plt.ylim(0,11)
plt.show()

#定义欧几里得距离
def distEuclid(x1,y1,x2,y2):
    d = sqrt((x1-x2)**2+(y1-y2)**2)
    return d

cent0 = [uniform(2,9),uniform(2,9)] #定义 K=3 个质心，随机赋值
cent1 = [uniform(2,9),uniform(2,9)] #[x,y]
cent2 = [uniform(2,9),uniform(2,9)]
mark = [] #标记列表
dist = [[],[],[]]#各质心到所有点的距离列表
#核心
for n in range(50):
    #计算各质心到所有点的距离
    for i in range(m):
        dist[0].append(distEuclid(cent0[0],cent0[1],data[0][i],data[1][i]))
        dist[1].append(distEuclid(cent1[0],cent1[1],data[0][i],data[1][i]))
        dist[2].append(distEuclid(cent2[0],cent2[1],data[0][i],data[1][i]))
    #对数据进行整理
    sum0_x = sum0_y = sum1_x = sum1_y = sum2_x = sum2_y = 0
    number0 = number1 = number2 = 0
    for i in range(m):
        if dist[0][i]dist[1][i] and dist[0][i]dist[2][i]:
            mark.append(0)
            sum0_x += data[0][i]
            sum0_y += data[1][i]
            number0 += 1
        elif dist[1][i]dist[0][i] and dist[1][i]dist[2][i]:
            mark.append(1)
            sum1_x += data[0][i]
            sum1_y += data[1][i]
            number1 += 1
        elif dist[2][i]dist[0][i] and dist[2][i]dist[1][i]:
            mark.append(2)
            sum2_x += data[0][i]
            sum2_y += data[1][i]
            number2 += 1    
    #更新质心
    cent0 = [sum0_x/number0,sum0_y/number0]
    cent1 = [sum1_x/number1,sum1_y/number1]
    cent2 = [sum2_x/number2,sum2_y/number2]

#画图
for i in range(m):
    if mark[i] == 0:
        plt.scatter(data[0][i],data[1][i],color='red')
    if mark[i] == 1:
        plt.scatter(data[0][i],data[1][i],color='blue')
    if mark[i] == 2:
        plt.scatter(data[0][i],data[1][i],color='green')     
plt.scatter(cent0[0],cent0[1],marker='*',color='red')
plt.scatter(cent1[0],cent1[1],marker='*',color='blue')
plt.scatter(cent2[0],cent2[1],marker='*',color='green')
plt.xlim(0,11)
plt.ylim(0,11)
plt.show()
在这里插入代码片

上述代码数据选择是随机生成的，每次运行结果是不同的，测试会发现出现分类不理想的效果。说明基础算法存在很大的弊端，我们需要改进，本篇内容为基础不做改进知识的说明。