主要就是了解一下pytorch中的使用layernorm这种归一化之后的数据变化，以及数据使用relu，prelu，leakyrelu之后的变化。

import torch
import torch.nn as nn
import torch.nn.functional as F
class model(nn.Module):
    def __init__(self):
        super(model, self).__init__()
        self.LN=nn.LayerNorm(10,eps=0,elementwise_affine=True)
        self.PRelu=nn.PReLU(init=0.25)
        self.Relu=nn.ReLU()
        self.LeakyReLU=nn.LeakyReLU(negative_slope=0.01,inplace=False)
    def forward(self,input ):
        out=self.LN(input)
        print("LN:",out)
        out1=self.PRelu(out)
        print("PRelu:",out1)
        out2=self.Relu(out)
        print("Relu:",out2)
        out3=self.LeakyReLU(out)
        print("LeakyRelu:",out3)
        return out
tensor=torch.tensor([-0.9,0.1,0,-0.1,0.9,-0.4,0.9,-0.5,0.8,0.1])
net=model()
print(tensor)
net(tensor)

输出：

tensor([-0.9000,  0.1000,  0.0000, -0.1000,  0.9000, -0.4000,  0.9000, -0.5000,
         0.8000,  0.1000])
LN: tensor([-1.6906,  0.0171, -0.1537, -0.3245,  1.3833, -0.8368,  1.3833, -1.0076,
         1.2125,  0.0171], grad_fn=NativeLayerNormBackward>)
Relu: tensor([0.0000, 0.0171, 0.0000, 0.0000, 1.3833, 0.0000, 1.3833, 0.0000, 1.2125,
        0.0171], grad_fn=ReluBackward0>)
PRelu: tensor([-0.4227,  0.0171, -0.0384, -0.0811,  1.3833, -0.2092,  1.3833, -0.2519,
         1.2125,  0.0171], grad_fn=PreluBackward>)
LeakyRelu: tensor([-0.0169,  0.0171, -0.0015, -0.0032,  1.3833, -0.0084,  1.3833, -0.0101,
         1.2125,  0.0171], grad_fn=LeakyReluBackward0>)

从上面可以看出，这个LayerNorm的归一化，并不是将数据限定在0-1之间，也没有进行一个类似于高斯分布一样的分数，只是将其进行了一个处理，对应的数值得到了一些变化，相同数值的变化也是相同的。

Relu的则是单纯将小于0的数变成了0，减少了梯度消失的可能性

PRelu是一定程度上的保留了负值，根据init给的值。

LeakyRelu也是一定程度上保留负值，不过比较小，应该是根据negative_slope给的值。

补充：PyTorch学习之归一化层（BatchNorm、LayerNorm、InstanceNorm、GroupNorm）

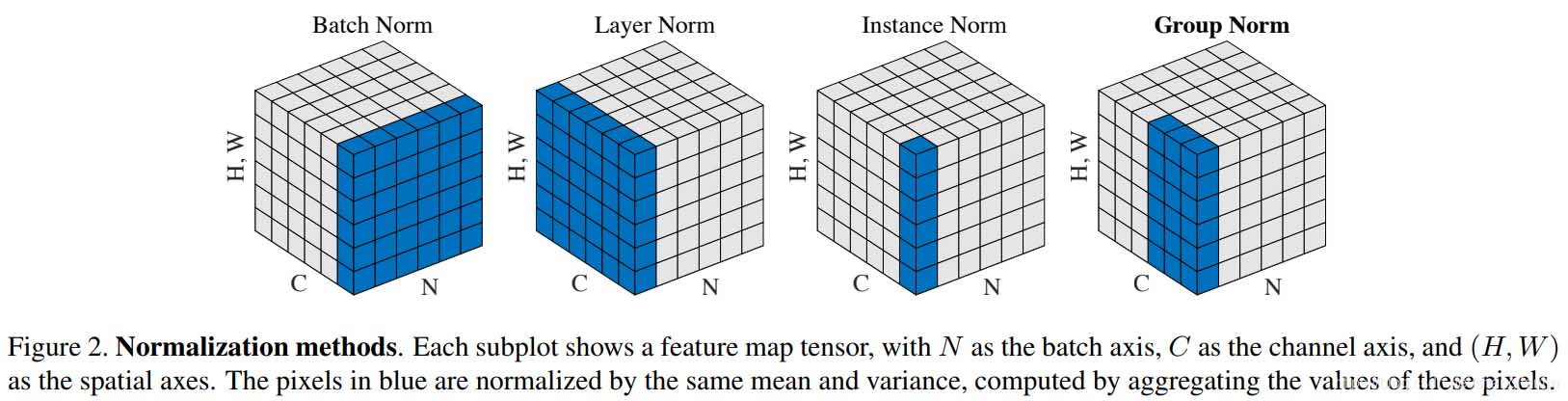
BN，LN，IN，GN从学术化上解释差异：

BatchNorm：batch方向做归一化，算NHW的均值，对小batchsize效果不好；BN主要缺点是对batchsize的大小比较敏感，由于每次计算均值和方差是在一个batch上，所以如果batchsize太小，则计算的均值、方差不足以代表整个数据分布

LayerNorm：channel方向做归一化，算CHW的均值，主要对RNN作用明显；

InstanceNorm：一个channel内做归一化，算H*W的均值，用在风格化迁移；因为在图像风格化中，生成结果主要依赖于某个图像实例，所以对整个batch归一化不适合图像风格化中，因而对HW做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。

GroupNorm：将channel方向分group，然后每个group内做归一化，算(C//G)HW的均值；这样与batchsize无关，不受其约束。

SwitchableNorm是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。

1 BatchNorm

torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

参数：

num_features： 来自期望输入的特征数，该期望输入的大小为'batch_size x num_features [x width]'

eps： 为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。

momentum： 动态均值和动态方差所使用的动量。默认为0.1。

affine： 布尔值，当设为true，给该层添加可学习的仿射变换参数。

track_running_stats：布尔值，当设为true，记录训练过程中的均值和方差；

实现公式：

track_running_stats：布尔值，当设为true，记录训练过程中的均值和方差；

实现公式：

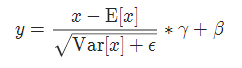
2 GroupNorm

torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)

参数：

num_groups：需要划分为的groups

num_features：来自期望输入的特征数，该期望输入的大小为'batch_size x num_features [x width]'

eps：为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。

momentum：动态均值和动态方差所使用的动量。默认为0.1。

affine：布尔值，当设为true，给该层添加可学习的仿射变换参数。

实现公式：

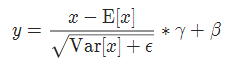
3 InstanceNorm

torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
torch.nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)

参数：

num_features：来自期望输入的特征数，该期望输入的大小为'batch_size x num_features [x width]'

eps：为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。

momentum：动态均值和动态方差所使用的动量。默认为0.1。

affine：布尔值，当设为true，给该层添加可学习的仿射变换参数。

track_running_stats：布尔值，当设为true，记录训练过程中的均值和方差；

实现公式：

4 LayerNorm

torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)

参数：

normalized_shape： 输入尺寸

[∗×normalized_shape[0]×normalized_shape[1]×…×normalized_shape[−1]]

eps： 为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。

elementwise_affine： 布尔值，当设为true，给该层添加可学习的仿射变换参数。

实现公式：

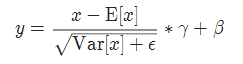
5 LocalResponseNorm

torch.nn.LocalResponseNorm(size, alpha=0.0001, beta=0.75, k=1.0)

参数：

size：用于归一化的邻居通道数

alpha：乘积因子，Default: 0.0001

beta ：指数，Default: 0.75

k：附加因子，Default: 1

实现公式：

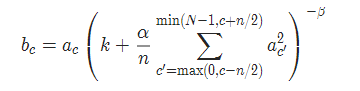
以上为个人经验，希望能给大家一个参考，也希望大家多多支持脚本之家。