算法系列15天速成第十一天树操作（上）-巨人网络通讯

算法系列15天速成第十一天树操作（上）

先前我们讲的都是“线性结构”，他的特征就是“一个节点最多有一个”前驱“和一个”后继“。那么我们今天讲的树会是怎样的呢？

我们可以对”线性结构“改造一下，变为”一个节点最多有一个"前驱“和”多个后继“。哈哈，这就是我们今天说的”树“。

一：树

我们思维中的”树“就是一种枝繁叶茂的形象，那么数据结构中的”树“该是怎么样呢？对的，他是一种现实中倒立的树。

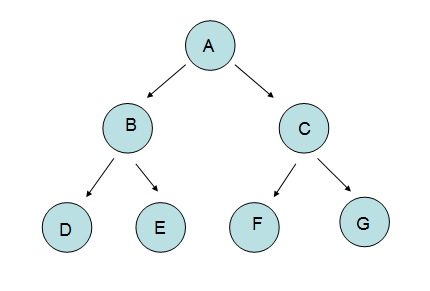
1：术语

其实树中有很多术语的，这个是我们学习树形结构必须掌握的。

1> 父节点，子节点，兄弟节点

这个就比较简单了，B和C的父节点就是A，反过来说就是B和C是A的子节点。B和C就是兄弟节点。

2> 结点的度

其实”度“就是”分支数“，比如A的分支数有两个“B和C",那么A的度为2。

3> 树的度

看似比较莫名其妙吧，他和”结点的度“的区别就是，树的度讲究大局观，乃树中最大的结点度，其实也就是2。

4> 叶结点，分支结点

叶结点就是既没有左孩子也没有右孩子结点，也就是结点度为0。分支节点也就是if的else的条件咯。

5> 结点的层数

这个很简单，也就是树有几层。

6> 有序树，无序树

有序树我们先前也用过，比如“堆”和“二叉排序树”，说明这种树是按照一定的规则进行排序的，else条件就是无序树。

7> 森林

现实中，很多的树形成了森林，那在数据结构中，我们把上图的“A”节点砍掉，那么B，C子树合一起就是森林咯。

2: 树的表示

树这个结构的表示其实有很多种，常用的也就是“括号”表示法。
比如上面的树就可以表示为：(A(B(D),(E)),(C(F),(G)))

二：二叉树

在我们项目开发中，很多地方都会用到树，但是多叉树的处理还是比较纠结的，所以俺们本着“大事化小，小事化了“的原则

把”多叉树“转化为”二叉树“，那么问题就简化了很多。

1： ”二叉树“和”树“有什么差异呢？

第一点: 树的度没有限制，而“二叉树”最多只能有两个，不然也就不叫二叉树了，哈哈。
第二点：树中的子树没有左右划分，很简单啊，找不到参照点，二叉树就有参照物咯。

2：二叉树的类型

二叉树中有两种比较完美的类型，“完全二叉树”和“满二叉树”。

1> 满二叉树

除叶子节点外，所有节点的度都为2，文章开头处的树就是这里的“满二叉树”。

2> 完全二叉树

必须要满足两个条件就即可：干掉最后一层，二叉树变为“满二叉树”。

最后一层的叶节点必须是“从左到右”依次排开。

我们干掉文章开头处的节点“F和”G",此时还是“完全二叉树”，但已经不是“满二叉树”了，你懂的。

3：二叉树的性质

二叉树中有5点性质非常重要，也是俺们必须要记住的。

1> 二叉树中，第i层的节点最多有2(i-1)个。

2> 深度为k的二叉树最多有2k-1个节点。

3> 二叉树中，叶子节点树为N1个，度为2的节点有N2个，那么N1=N2+1。

4> 具有N个结点的二叉树深度为（Log2 N）+1层。

5> N个结点的完全二叉树如何用顺序存储，对于其中的一个结点i，存在以下关系，

2*i是结点i的父结点。

i/2是结点i的左孩子。

(i/2)+1是结点i的右孩子。

4：二叉树的顺序存储

同样的存储方式也有两种，“顺序存储”和“链式存储”。

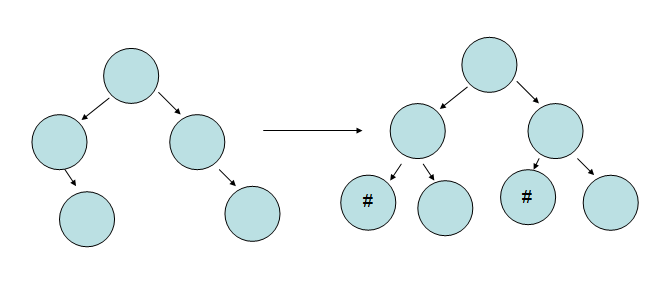
1> 顺序存储

说实话，树的存储用顺序结构比较少，因为从性质定理中我们都可以看出只限定为“完全二叉树”，那么如果二叉树不是

“完全二叉树”，那我们就麻烦了，必须将其转化为“完全二叉树”，将空的节点可以用“#”代替，图中也可看出，为了维护

性质定理5的要求，我们牺牲了两个”资源“的空间。

2> 链式存储

上面也说了，顺序存储会造成资源的浪费，所以嘛，我们开发中用的比较多的还是“链式存储”，同样“链式存储”

也非常的形象，非常的合理。

一个结点存放着一个“左指针”和一个“右指针”，这就是二叉链表。

如何方便的查找到该结点的父结点，可以采用三叉链表。

5: 常用操作

一般也就是“添加结点“，“查找节点”，“计算深度”，“遍历结点”，“清空结点”

1> 这里我们就用二叉链表来定义链式存储模型

复制代码代码如下:

#region 二叉链表存储结构
    /// summary>
/// 二叉链表存储结构
/// /summary>
/// typeparam name="T">/typeparam>
    public class ChainTreeT>
    {
        public T data;

public ChainTreeT> left;

        public ChainTreeT> right;
    }
    #endregion

2> 添加结点

要添加结点，我们就要找到添加结点的父结点，并且根据指示插入到父结点中指定左结点或者右结点。

复制代码代码如下:

#region 将指定节点插入到二叉树中
        /// summary>
/// 将指定节点插入到二叉树中
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="node">/param>
/// param name="direction">插入做左是右/param>
/// returns>/returns>
        public ChainTreeT> BinTreeAddNodeT>(ChainTreeT> tree, ChainTreeT> node, T data, Direction direction)
        {
            if (tree == null)
                return null;

            if (tree.data.Equals(data))
            {
                switch (direction)
                {
                    case Direction.Left:
                        if (tree.left != null)
                            throw new Exception("树的左节点不为空，不能插入");
                        else
                            tree.left = node;

                        break;
                    case Direction.Right:
                        if (tree.right != null)
                            throw new Exception("树的右节点不为空，不能插入");
                        else
                            tree.right = node;

                        break;
                }
            }

BinTreeAddNode(tree.left, node, data, direction);
BinTreeAddNode(tree.right, node, data, direction);

            return tree;
        }
        #endregion

3> 查找节点

二叉树中到处都散发着递归思想，很能锻炼一下我们对递归的认识，同样查找也是用到了递归思想。

复制代码代码如下:

#region 在二叉树中查找指定的key
        /// summary>
///在二叉树中查找指定的key
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="data">/param>
/// returns>/returns>
        public ChainTreeT> BinTreeFindT>(ChainTreeT> tree, T data)
        {
            if (tree == null)
                return null;

if (tree.data.Equals(data))
return tree;

            return BinTreeFind(tree, data);
        }
        #endregion

4> 计算深度

这个问题纠结了我二个多小时，原因在于没有深刻的体会到递归，其实主要思想就是递归左子树和右子树，然后得出较大的一个。

复制代码代码如下:

#region 获取二叉树的深度
        /// summary>
/// 获取二叉树的深度
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// returns>/returns>
        public int BinTreeLenT>(ChainTreeT> tree)
        {
            int leftLength;
            int rightLength;

if (tree == null)
return 0;

//递归左子树的深度
leftLength = BinTreeLen(tree.left);

//递归右子书的深度
rightLength = BinTreeLen(tree.right);

            if (leftLength > rightLength)
                return leftLength + 1;
            else
                return rightLength + 1;
        }
        #endregion

5> 遍历结点

二叉树中遍历节点的方法还是比较多的，有“先序”，“中序”，“后序”，“按层”，其实这些东西只可意会，不可言传，真的很难在口头

上说清楚，需要反复的体会递归思想。

先序：先访问根，然后递归访问左子树，最后递归右子树。（DLR模式）

中序：先递归访问左子树，在访问根，最后递归右子树。（LDR模式）

后序：先递归访问左子树，然后递归访问右子树，最后访问根。（LRD模式）

按层：这个比较简单，从上到下，从左到右的遍历节点。

复制代码代码如下:

#region 二叉树的先序遍历
        /// summary>
/// 二叉树的先序遍历
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
        public void BinTree_DLRT>(ChainTreeT> tree)
        {
            if (tree == null)
                return;

//先输出根元素
Console.Write(tree.data + "\t");

//然后遍历左子树
BinTree_DLR(tree.left);

            //最后遍历右子树
            BinTree_DLR(tree.right);
        }
        #endregion

        #region 二叉树的中序遍历
        /// summary>
/// 二叉树的中序遍历
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
        public void BinTree_LDRT>(ChainTreeT> tree)
        {
            if (tree == null)
                return;

//优先遍历左子树
BinTree_LDR(tree.left);

//然后输出节点
Console.Write(tree.data + "\t");

            //最后遍历右子树
            BinTree_LDR(tree.right);
        }
        #endregion

        #region 二叉树的后序遍历
        /// summary>
/// 二叉树的后序遍历
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
        public void BinTree_LRDT>(ChainTreeT> tree)
        {
            if (tree == null)
                return;

//优先遍历左子树
BinTree_LRD(tree.left);

//然后遍历右子树
BinTree_LRD(tree.right);

            //最后输出节点元素
            Console.Write(tree.data + "\t");
        }
        #endregion

        #region 二叉树的按层遍历
        /// summary>
/// 二叉树的按层遍历
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
        public void BinTree_LevelT>(ChainTreeT> tree)
        {
            if (tree == null)
                return;

//申请保存空间
ChainTreeT>[] treeList = new ChainTreeT>[Length];

int head = 0;
int tail = 0;

//存放数组
treeList[tail] = tree;

//循环链中计算tail位置
tail = (tail + 1) % Length;

            while (head != tail)
            {
                var tempNode = treeList[head];

head = (head + 1) % Length;

//输出节点
Console.Write(tempNode.data + "\t");

                //如果左子树不为空,则将左子树存于数组的tail位置
                if (tempNode.left != null)
                {
                    treeList[tail] = tempNode.left;

tail = (tail + 1) % Length;
}

                //如果右子树不为空，则将右子树存于数组的tail位置
                if (tempNode.right != null)
                {
                    treeList[tail] = tempNode.right;

                    tail = (tail + 1) % Length;
                }
            }
        }
        #endregion

6> 清空二叉树

虽然C#里面有GC，但是我们能自己释放的就不麻烦GC了，同样清空二叉树节点，我们用到了递归，说实话，这次练习让我喜欢

上的递归，虽然XXX的情况下，递归的不是很好，但是递归还是很强大的。

复制代码代码如下:

#region 清空二叉树
        /// summary>
/// 清空二叉树
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
        public void BinTreeClearT>(ChainTreeT> tree)
        {
            //递的结束点，归的起始点
            if (tree == null)
                return;

BinTreeClear(tree.left);
BinTreeClear(tree.right);

            //在归的过程中，释放当前节点的数据空间
            tree = null;
        }
        #endregion

最后上一下总的代码

复制代码代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace ChainTree
{
    public class Program
    {
        static void Main(string[] args)
        {
            ChainTreeManager manager = new ChainTreeManager();

//插入节点操作
ChainTreestring> tree = CreateRoot();

//插入节点数据
AddNode(tree);

            //先序遍历
            Console.WriteLine("\n先序结果为： \n");
            manager.BinTree_DLR(tree);

            //中序遍历
            Console.WriteLine("\n中序结果为： \n");
            manager.BinTree_LDR(tree);

            //后序遍历
            Console.WriteLine("\n后序结果为： \n");
            manager.BinTree_LRD(tree);

            //层次遍历
            Console.WriteLine("\n层次结果为： \n");
            manager.Length = 100;
            manager.BinTree_Level(tree);

Console.WriteLine("\n树的深度为：" + manager.BinTreeLen(tree) + "\n");

Console.ReadLine();

}

        #region 生成根节点
        /// summary>
/// 生成根节点
/// /summary>
/// returns>/returns>
        static ChainTreestring> CreateRoot()
        {
            ChainTreestring> tree = new ChainTreestring>();

Console.WriteLine("请输入根节点，方便我们生成树\n");

tree.data = Console.ReadLine();

Console.WriteLine("根节点生成已经生成\n");

            return tree;
        }
        #endregion

        #region 插入节点操作
        /// summary>
/// 插入节点操作
/// /summary>
/// param name="tree">/param>
        static ChainTreestring> AddNode(ChainTreestring> tree)
        {
            ChainTreeManager mananger = new ChainTreeManager();

            while (true)
            {
                ChainTreestring> node = new ChainTreestring>();

Console.WriteLine("请输入要插入节点的数据：\n");

node.data = Console.ReadLine();

Console.WriteLine("请输入要查找的父节点数据：\n");

var parentData = Console.ReadLine();

                if (tree == null)
                {
                    Console.WriteLine("未找到您输入的父节点，请重新输入。");
                    continue;
                }

Console.WriteLine("请确定要插入到父节点的：1 左侧，2 右侧");

Direction direction = (Direction)Enum.Parse(typeof(Direction), Console.ReadLine());

tree = mananger.BinTreeAddNode(tree, node, parentData, direction);

Console.WriteLine("插入成功，是否继续？ 1 继续， 2 退出");

                if (int.Parse(Console.ReadLine()) == 1)
                    continue;
                else
                    break;
            }

            return tree;
        }
        #endregion
    }

    #region 插入左节点或者右节点
    /// summary>
/// 插入左节点或者右节点
/// /summary>
    public enum Direction { Left = 1, Right = 2 }
    #endregion

    #region 二叉链表存储结构
    /// summary>
/// 二叉链表存储结构
/// /summary>
/// typeparam name="T">/typeparam>
    public class ChainTreeT>
    {
        public T data;

public ChainTreeT> left;

        public ChainTreeT> right;
    }
    #endregion

    /// summary>
/// 二叉树的操作帮助类
/// /summary>
    public class ChainTreeManager
    {
        #region 按层遍历的Length空间存储
        /// summary>
/// 按层遍历的Length空间存储
/// /summary>
        public int Length { get; set; }
        #endregion

                        break;
                }
            }

BinTreeAddNode(tree.left, node, data, direction);
BinTreeAddNode(tree.right, node, data, direction);

            return tree;
        }
        #endregion

        #region 获取二叉树指定孩子的状态
        /// summary>
/// 获取二叉树指定孩子的状态
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="direction">/param>
/// returns>/returns>
        public ChainTreeT> BinTreeChildT>(ChainTreeT> tree, Direction direction)
        {
            ChainTreeT> childNode = null;

if (tree == null)
throw new Exception("二叉树为空");

            switch (direction)
            {
                case Direction.Left:
                    childNode = tree.left;
                    break;
                case Direction.Right:
                    childNode = tree.right;
                    break;
            }

return childNode;
}

#endregion

if (tree == null)
return 0;

//递归左子树的深度
leftLength = BinTreeLen(tree.left);

//递归右子书的深度
rightLength = BinTreeLen(tree.right);

            if (leftLength > rightLength)
                return leftLength + 1;
            else
                return rightLength + 1;
        }
        #endregion

        #region 判断二叉树是否为空
        /// summary>
/// 判断二叉树是否为空
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// returns>/returns>
        public bool BinTreeisEmptyT>(ChainTreeT> tree)
        {
            return tree == null ? true : false;
        }
        #endregion

if (tree.data.Equals(data))
return tree;

            return BinTreeFind(tree, data);
        }
        #endregion

BinTreeClear(tree.left);
BinTreeClear(tree.right);

            //在归的过程中，释放当前节点的数据空间
            tree = null;
        }
        #endregion

//先输出根元素
Console.Write(tree.data + "\t");

//然后遍历左子树
BinTree_DLR(tree.left);

            //最后遍历右子树
            BinTree_DLR(tree.right);
        }
        #endregion

//优先遍历左子树
BinTree_LDR(tree.left);

//然后输出节点
Console.Write(tree.data + "\t");

            //最后遍历右子树
            BinTree_LDR(tree.right);
        }
        #endregion

//优先遍历左子树
BinTree_LRD(tree.left);

//然后遍历右子树
BinTree_LRD(tree.right);

            //最后输出节点元素
            Console.Write(tree.data + "\t");
        }
        #endregion

//申请保存空间
ChainTreeT>[] treeList = new ChainTreeT>[Length];

int head = 0;
int tail = 0;

//存放数组
treeList[tail] = tree;

//循环链中计算tail位置
tail = (tail + 1) % Length;

            while (head != tail)
            {
                var tempNode = treeList[head];

head = (head + 1) % Length;

//输出节点
Console.Write(tempNode.data + "\t");

                //如果左子树不为空,则将左子树存于数组的tail位置
                if (tempNode.left != null)
                {
                    treeList[tail] = tempNode.left;

tail = (tail + 1) % Length;
}

                //如果右子树不为空，则将右子树存于数组的tail位置
                if (tempNode.right != null)
                {
                    treeList[tail] = tempNode.right;

                    tail = (tail + 1) % Length;
                }
            }
        }
        #endregion

}
}

我们把文章开头的“二叉树”的节点输入到我们的结构中，看看遍历效果咋样。