直接插入排序:
这种排序其实蛮好理解的,很现实的例子就是俺们斗地主,当我们抓到一手乱牌时,我们就要按照大小梳理扑克,30秒后,
扑克梳理完毕,4条3,5条s,哇塞...... 回忆一下,俺们当时是怎么梳理的。
最左一张牌是3,第二张牌是5,第三张牌又是3,赶紧插到第一张牌后面去,第四张牌又是3,大喜,赶紧插到第二张后面去,
第五张牌又是3,狂喜,哈哈,一门炮就这样产生了。
怎么样,生活中处处都是算法,早已经融入我们的生活和血液。
下面就上图说明: 
看这张图不知道大家可否理解了,在插入排序中,数组会被划分为两种,“有序数组块”和“无序数组块”,
对的,第一遍的时候从”无序数组块“中提取一个数20作为有序数组块。
第二遍的时候从”无序数组块“中提取一个数60有序的放到”有序数组块中“,也就是20,60。
第三遍的时候同理,不同的是发现10比有序数组的值都小,因此20,60位置后移,腾出一个位置让10插入。
然后按照这种规律就可以全部插入完毕。
复制代码 代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace InsertSort
{
public class Program
{
static void Main(string[] args)
{
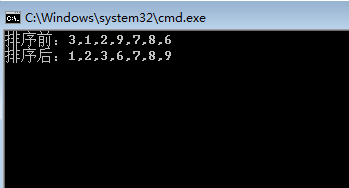
Listint> list = new Listint>() { 3, 1, 2, 9, 7, 8, 6 };
Console.WriteLine("排序前:" + string.Join(",", list));
InsertSort(list);
Console.WriteLine("排序后:" + string.Join(",", list));
}
static void InsertSort(Listint> list)
{
//无须序列
for (int i = 1; i list.Count; i++)
{
var temp = list[i];
int j;
//有序序列
for (j = i - 1; j >= 0 temp list[j]; j--)
{
list[j + 1] = list[j];
}
list[j + 1] = temp;
}
}
}
}
希尔排序:
观察一下”插入排序“:其实不难发现她有个缺点:
如果当数据是”5, 4, 3, 2, 1“的时候,此时我们将“无序块”中的记录插入到“有序块”时,估计俺们要崩盘,
每次插入都要移动位置,此时插入排序的效率可想而知。
shell根据这个弱点进行了算法改进,融入了一种叫做“缩小增量排序法”的思想,其实也蛮简单的,不过有点注意的就是:
增量不是乱取,而是有规律可循的。
首先要明确一下增量的取法:
第一次增量的取法为: d=count/2;
第二次增量的取法为: d=(count/2)/2;
最后一直到: d=1;
看上图观测的现象为:
d=3时:将40跟50比,因50大,不交换。
将20跟30比,因30大,不交换。
将80跟60比,因60小,交换。
d=2时:将40跟60比,不交换,拿60跟30比交换,此时交换后的30又比前面的40小,又要将40和30交换,如上图。
将20跟50比,不交换,继续将50跟80比,不交换。
d=1时:这时就是前面讲的插入排序了,不过此时的序列已经差不多有序了,所以给插入排序带来了很大的性能提高。
既然说“希尔排序”是“插入排序”的改进版,那么我们就要比一下,在1w个数字中,到底能快多少?
下面进行一下测试:
复制代码 代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;
namespace ShellSort
{
public class Program
{
static void Main(string[] args)
{
//5次比较
for (int i = 1; i = 5; i++)
{
Listint> list = new Listint>();
//插入1w个随机数到数组中
for (int j = 0; j 10000; j++)
{
Thread.Sleep(1);
list.Add(new Random((int)DateTime.Now.Ticks).Next(10000, 1000000));
}
Listint> list2 = new Listint>();
list2.AddRange(list);
Console.WriteLine("\n第" + i + "次比较:");
Stopwatch watch = new Stopwatch();
watch.Start();
InsertSort(list);
watch.Stop();
Console.WriteLine("\n插入排序耗费的时间:" + watch.ElapsedMilliseconds);
Console.WriteLine("输出前十个数:" + string.Join(",", list.Take(10).ToList()));
watch.Restart();
ShellSort(list2);
watch.Stop();
Console.WriteLine("\n希尔排序耗费的时间:" + watch.ElapsedMilliseconds);
Console.WriteLine("输出前十个数:" + string.Join(",", list2.Take(10).ToList()));
}
}
///summary>
/// 希尔排序
////summary>
///param name="list">/param>
static void ShellSort(Listint> list)
{
//取增量
int step = list.Count / 2;
while (step >= 1)
{
//无须序列
for (int i = step; i list.Count; i++)
{
var temp = list[i];
int j;
//有序序列
for (j = i - step; j >= 0 temp list[j]; j = j - step)
{
list[j + step] = list[j];
}
list[j + step] = temp;
}
step = step / 2;
}
}
///summary>
/// 插入排序
////summary>
///param name="list">/param>
static void InsertSort(Listint> list)
{
//无须序列
for (int i = 1; i list.Count; i++)
{
var temp = list[i];
int j;
//有序序列
for (j = i - 1; j >= 0 temp list[j]; j--)
{
list[j + 1] = list[j];
}
list[j + 1] = temp;
}
}
}
}
截图如下:
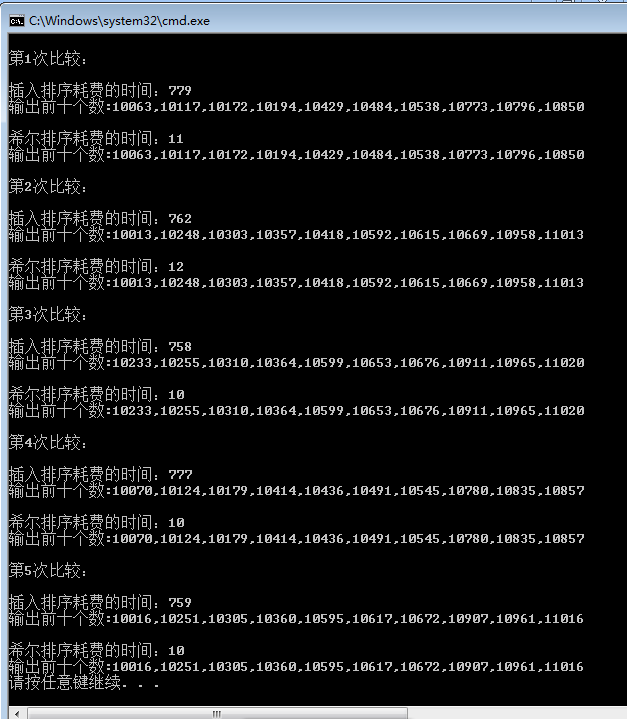
看的出来,希尔排序优化了不少,w级别的排序中,相差70几倍哇。
归并排序:
个人感觉,我们能容易看的懂的排序基本上都是O (n^2),比较难看懂的基本上都是N(LogN),所以归并排序也是比较难理解的,尤其是在代码
编写上,本人就是搞了一下午才搞出来,嘻嘻。
首先看图:
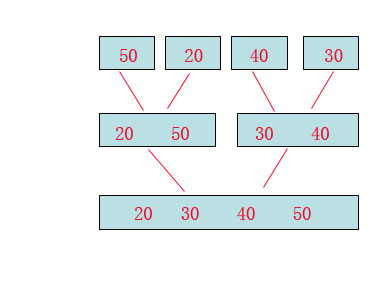
归并排序中中两件事情要做:
第一: “分”, 就是将数组尽可能的分,一直分到原子级别。
第二: “并”,将原子级别的数两两合并排序,最后产生结果。
代码:
复制代码 代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace MergeSort
{
class Program
{
static void Main(string[] args)
{
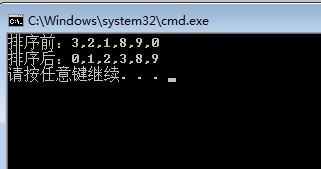
int[] array = { 3, 2, 1, 8, 9, 0 };
MergeSort(array, new int[array.Length], 0, array.Length - 1);
Console.WriteLine(string.Join(",", array));
}
///summary>
/// 数组的划分
////summary>
///param name="array">待排序数组/param>
///param name="temparray">临时存放数组/param>
///param name="left">序列段的开始位置,/param>
///param name="right">序列段的结束位置/param>
static void MergeSort(int[] array, int[] temparray, int left, int right)
{
if (left right)
{
//取分割位置
int middle = (left + right) / 2;
//递归划分数组左序列
MergeSort(array, temparray, left, middle);
//递归划分数组右序列
MergeSort(array, temparray, middle + 1, right);
//数组合并操作
Merge(array, temparray, left, middle + 1, right);
}
}
///summary>
/// 数组的两两合并操作
////summary>
///param name="array">待排序数组/param>
///param name="temparray">临时数组/param>
///param name="left">第一个区间段开始位置/param>
///param name="middle">第二个区间的开始位置/param>
///param name="right">第二个区间段结束位置/param>
static void Merge(int[] array, int[] temparray, int left, int middle, int right)
{
//左指针尾
int leftEnd = middle - 1;
//右指针头
int rightStart = middle;
//临时数组的下标
int tempIndex = left;
//数组合并后的length长度
int tempLength = right - left + 1;
//先循环两个区间段都没有结束的情况
while ((left = leftEnd) (rightStart = right))
{
//如果发现有序列大,则将此数放入临时数组
if (array[left] array[rightStart])
temparray[tempIndex++] = array[left++];
else
temparray[tempIndex++] = array[rightStart++];
}
//判断左序列是否结束
while (left = leftEnd)
temparray[tempIndex++] = array[left++];
//判断右序列是否结束
while (rightStart = right)
temparray[tempIndex++] = array[rightStart++];
//交换数据
for (int i = 0; i tempLength; i++)
{
array[right] = temparray[right];
right--;
}
}
}
}
结果图:
ps: 插入排序的时间复杂度为:O(N^2)
希尔排序的时间复杂度为:平均为:O(N^3/2)
最坏: O(N^2)
归并排序时间复杂度为: O(NlogN)
空间复杂度为: O(N)
您可能感兴趣的文章:- 算法系列15天速成 第十四天 图【上】
- 算法系列15天速成——第十三天 树操作【下】
- 算法系列15天速成 第十二天 树操作【中】
- 算法系列15天速成 第十一天 树操作(上)
- 算法系列15天速成 第十天 栈
- 算法系列15天速成 第八天 线性表【下】
- 算法系列15天速成 第九天 队列
- 算法系列15天速成 第七天 线性表【上】
- 算法系列15天速成 第六天 五大经典查找【下】
- 算法系列15天速成 第五天 五大经典查找【中】
- 算法系列15天速成 第四天 五大经典查找【上】
- 算法系列15天速成 第二天 七大经典排序【中】
- 算法系列15天速成 第一天 七大经典排序【上】
- 算法系列15天速成——第十五天 图【下】(大结局)
 咨 询 客 服
咨 询 客 服